Meta MMM Robyn Walkthrough 05 - 로빈 모델 원페이저 해석 Part 1
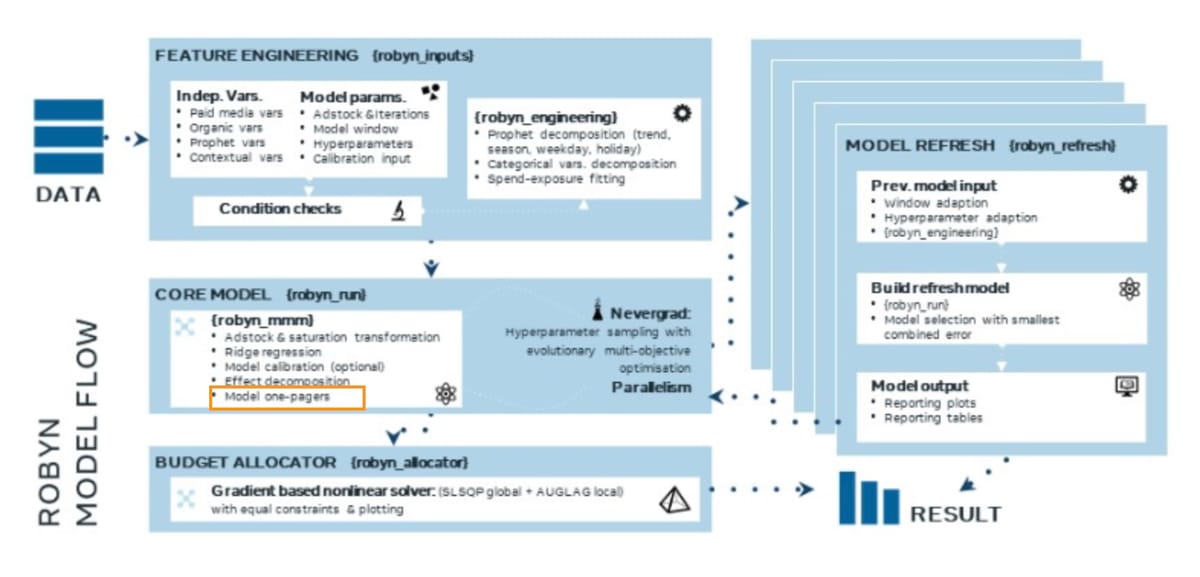
지난번까지 한 것은 구성했던 초기 모델을 한번 돌려보는 것이었습니다. 이 결과로 특징이 유사한 클러스터들이 만들어지고, 로빈은 이 클러스터들 중에서 성능이 가장 좋은 모델들을 대상으로 모델의 특성을 요약한 '원페이저'를 생성합니다. 우리가 해야 할 것은 이 들 중 실제로 사용할 모델을 선별하는 것인데요, 그래서 이를 위해 원페이저를 보고 해석할 수 있어야 합니다. 이번에 다룰 내용이 이것입니다.
Model One-pager 공식 설명
공식 튜토리얼인 demo.R 파일에는 원페이저에 대한 설명이 없습니다. 그래도 Meta의 Robyn 깃헙에는 이에 대한 설명이 있으니 참고를 해보는 것도 좋습니다. 특히 로빈 버전이 올라가면 원페이저 내용이 달라지는 경우도 있어서, 이 공식 설명은 가끔식 살펴볼 필요는 있습니다. 아래 링크입니다.
설명이 영어로 되어 있고 길어서 간단하게만 요약 하면 다음과 같습니다. 해석은 다음 섹션에서 하겠습니다.
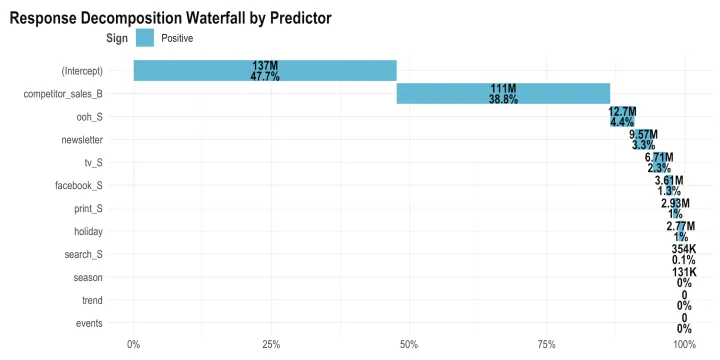
Response decomposition waterfall
아마도 모두들 가장 궁금해할 데이터일 것이라서 첫 번째로 보여주는 차트일 것입니다. 각 매체별로 수익에 얼마만큼 기여 했는지를 모델링한 데이터입니다.
Actual vs. predicted response
오렌지색 라인이 실제 매출액, 파란색 라인이 모델이 예측한 매출액입니다. 이 두 라인이 갭이 적고 비슷한 움직임을 보일수록 모델이 잘 학습 되었다고 볼 수 있습니다.
Share of spend vs. share of effect
1번 차트에서 매출 기여도가 나왔죠. 이것을 매체별 비용 데이터로 연산하여 ROAS를 표현한 차트입니다.
In-cluster bootstrapped confidence interval
한 클러스터 내의 모델들이 각 채널마다 ROAS를 예측하는데요, 이것이 얼마나 신뢰할 수 있을지를 판단해 볼 수 있는 차트입니다. 이를 위해 부트스트래핑 이라는 통계 기법을 사용합니다. 단어 자체는 생소하지만 결국 클러스터 내에서 무작위 샘플링을 해서 데이터를 뽑아낸 다음 분포를 봅니다. 아래쪽에서 조금더 자세하게 설명하려 합니다.
Adstock decay rate
Geometric의 경우 여기에 나온 % 만큼의 효과가 다음 기간으로 이월되도록 모델이 계산했다는 의미입니다. 예를 들어 30%라면, 한 주에 지출한 비용의 30%만큼의 효과가 다음 주로 이월된다는 의미입니다.
Immediate vs. carryover
각 미디어가 만들어낸 전체 효과 중 즉시 발생한 효과와 이월되어 나타난 효과가 각각 어느정도 비중을 차지하는지 보여주는 차트입니다.
Saturation curves
차트에는 Response curve로 표시되어있는데요, 미디어 포화도를 보여주는 부분입니다. 커브의 굴곡이 평평해진다면 더이상 예산을 투입해도 매출 상승을 기대하기 어려운 포화상태에 가까운 것입니다. 반대로 굴곡이 가파르다면 예산을 더 투입해도 좋은 상태로 해석할 수 있습니다.
Fitted vs. residual
모델의 예측치가 얼마나 적합한지 또는 차이가 큰지를 볼 수 있습니다. 전반적으로는 데이터가 x축에 붙어서 나란히 있는 것이 가장 이상적이고, 차트에서 웨이브나 퍼널이 클수록 적합도가 떨어지는 영역이 있는 것입니다.
특정 모델의 원페이저 해석 Part 1
제가 돌린 모델링에서 로빈이 출력한 3_204_6 모델의 원페이저를 기준으로 결과를 해석해보겠습니다. 원페이저 원본은 사이즈가 커서 리사이즈해서 올립니다. webp로 압축해도 파일 크기가 상당하네요.
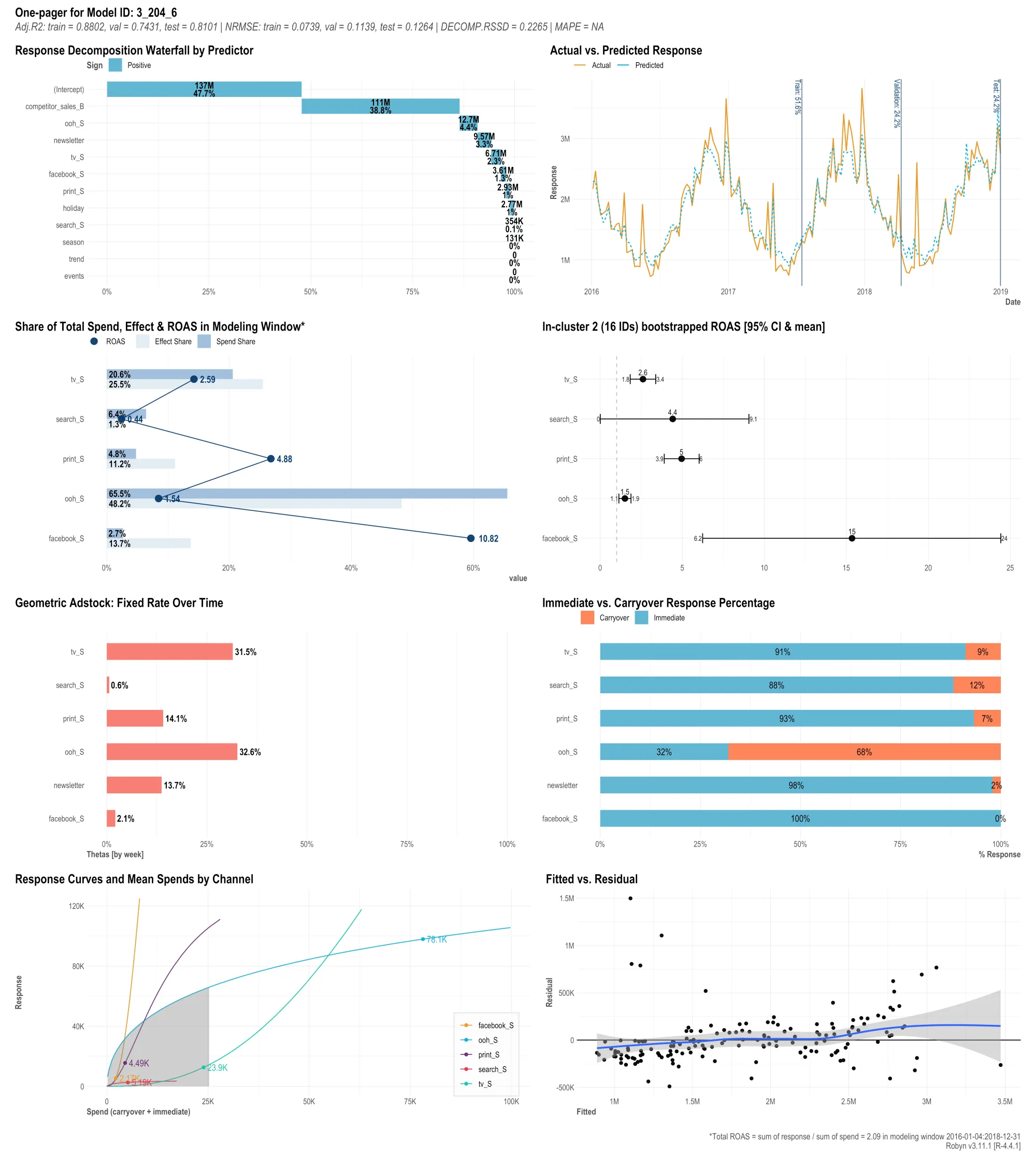
종합
모델 3_204_6은 학습이 잘 되어있고 테스트 데이터에 대해서도 좋은 결과를 보입니다. 그래서 앞으로 발생할 실제 데이터를 예측하는 것도 잘 해낼 것으로, 즉 좋은 일반화 성능을 보여줄 것으로 기대할만 합니다. 원페이저에 있는 아래 수치들이 그 근거입니다.
- Adjusted R2: train = 0.8802, val = 0.7431, test =0.8101
- NRMSE: train = 0.0739, val = 0.1139, test = 0.1264
- DECOMP.RSSD = 0.2265
각 평가 지표들이 학습, 검증, 테스트 데이터셋에 대해서 점수를 산출했습니다. 이 항목들에 대한 해석을 내리실 수 있도록 아래에 보충 설명을 덧붙입니다.
Adj. R2
기본적으로 R2(R Square)는 회귀 모델에 적용합니다. 종속 변수의 변동을 독립 변수가 얼마나 잘 '설명'하느냐를 수치화 한 것입니다. 종속 변수는 우리가 예측 목표로 삼은 데이터를 말하며, 이번 케이스에선 수익(revenue)입니다. 모델 세팅 할 때 dep_var 로 "revenue"를 설정했었죠. 독립 변수는 그 외 다른 데이터들입니다. R2는 0 ~ 1 사이로 결과가 나오고 1에 가까울수록 설명력이 높은 것입니다. Adjusted R2는 이번 케이스처럼 독립 변수 숫자가 많을때 사용합니다.
NRMSE
Normalized Root Mean Squared Error는 모델의 예측 오차를 측정하는 지표 중 하나로, 특히 머신 러닝 분야처럼 상당히 다양한 데이터셋이 사용되는 경우에 적용하기 좋습니다. 오차(error)를 제곱(squered)해서 숫자를 양수로 바꿈과 동시에, 큰 오차일수록 제곱하는 과정에서 수치가 급수로 증가하며 패널티도 크게 부여됩니다. 이것을 평균(mean)을 내고 루트를 씌워서(root) 제곱했던 스케일을 다시 원래 수준으로 돌립니다. 여기에 정규화(nomarlized)를 더해서 이 데이터셋에서 나온 에러가 일반적인 기준에서는 어느 정도 수준인지를 평가합니다. 값이 0.1이라면 에러가 10% 수준이라는 것으로, 이 이하의 값이 나올수록 좋습니다.
DECOMP.RSSD
Decomposition Root Sum Squared Distance의 약자입니다. 각 모델이 예측한 결과가 일부 독립 변수의 데이터에 의존하고 있는 것인지, 또는 모든 독립 변수를 고르고 균형있게 고려한 결과인지를 평가할 수 있는 지표입니다. 개인적으로 여기에서 가장 중요한 것은 '무엇과 무엇의 distance를 구하는지 이해하는 것'이라고 생각합니다. 쉽게는 모든 독립 변수들이 만들어낸 매출 기여도의 평균과, 특정 독립 변수가 만들어낸 매출 기여도의 차이를 구한다고 이해하면 됩니다. 역시나 수치가 0에 가까울수록 좋습니다.
마치며 - 다음 단계
원페이저의 종합 결과까지 확인했습니다. 그 아래쪽으로 8개의 상세 그래프가 더 있죠. 다음 글에서는 이 8개 그래프를 해석해보겠습니다.

Comments ()